如何实现递增有序线性表中查找与插入X操作

线性表(a1,a2,a3,……,an)中元素递增有序且按顺序存储于计算机内。要求设计一算法完成用最少时间在表中查找数值为X的元素，若找到将其与后继元素位置相交换，若找不到将其插入表中并使表中元素仍递增有序。

这道题重点信息是线性表有序，即数组有序，同时还要求用最少的时间查找表中值为X的元素。这时，我们可以考虑采用折半查找，因为表的序性决定了其采用折半查找。若表中的元素是无序的，只能采用其它的方法了，时间复杂复为O(n)。

下面博主画了一个有序数组，假设里面有N个元素。其中要找到X跟X后继交换位置。

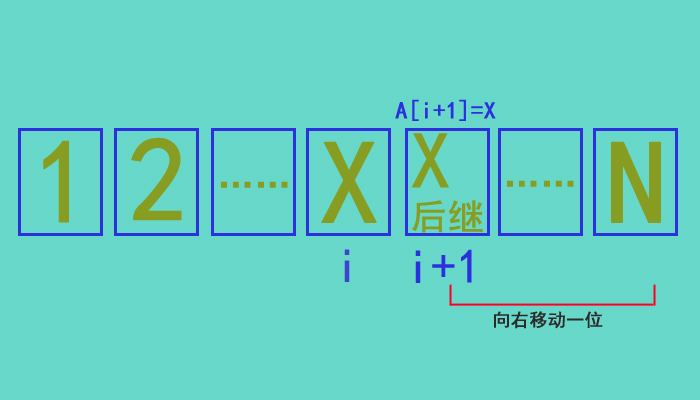
如何进行折半查找呢？

假设下面给出了一个递增有序的数组，如下图:

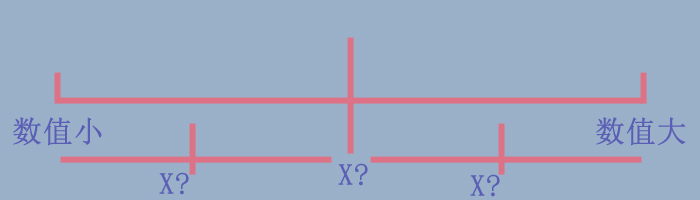
首先，取其中点，观察是不是要找的X元素，若是直接结束程序；若比X小，则要在X的右半部分查找，取其中点，看看是不是X；若比X大，则要在X左半部分查找，取其中点，看看是不是X。这样循环往复查找下去，直到找到X值为止。若查找完后，没有X值，说明查找失败。

下面是实现折半查找的核心程序：

int BinarySearch(ElemType x) // 则半查找元素x，核心元素
{
	int low = 0,high = n-1,mid; // low和high 指向顺序表下界和上界的下标
	while(low<=high)
	{
		mid = (low+high) / 2; // 找中间位置
		if(A[mid == x]) return mid; // 查找成功，返回mid,退出函数
		else if (A[mid] < x) low = mid + 1;//到中点mid右半部分查找
		else high = mid - 1;//到中点mid左半部分查找
	}
	return -1;// 查找失败，返回-1,退出函数
}

最终实现的函数：

void SearchExchangeInsert(ElemType A[],ElemType x)
{
	int mid,temp;
	mid = BinarySearch(x);
	// 下面两个if语句只会执行一个
	if(mid!=-1&&mid!=n-1) // 若存在x且不是最后的元素,那么可以进行元素的交换;
										  // 若存在x且是最后元素,那么程序直接结束;
	{
	temp = A[mid];A[mid] = A[mid + 1];A[mid + 1] = temp;
	}
	if(mid == -1) // 不存在x，则插入
	for(i = n-1;A[i] > x;i--) // 所有比x大的元素整体向右移动一位。
	A[i + 1] = A[i];
	A[i + 1] = x; // 插入x
}