数据结构的时间和空间复杂度详细总结

一、时间复杂度定义

• 它是用来衡量算法随着问题规模增大，算法执行时间增长的快慢
• 是问题规模的函数：T(n)是时间规模函数；时间复杂度主要分析T(n)的数量级
• T(n)=O(f(n)) f(n)是算法中基本运算的频度 一般我们考虑最坏情况下的时间复杂度

计算方法：取算法时间增长最快的那个函数项，忽略它的系数

二、空间复杂度定义

• 它用来衡量算法随着问题规模增大，算法所需空间的快慢
• 是问题规模的函数：S(n)=O(g(n)) ；算法所需空间的增长率和g(n)的增长率相同

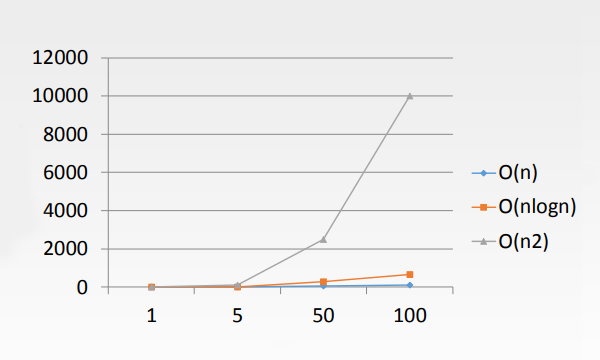
从图中，可以看到：随着问题规模的增大（横坐标），所需时间的增长率（斜率）差别很大。而且，这种差距随着问题规模的增大而显著地增大。

我们关心的就是算法的这个增长规模速度

三、常用的时间复杂度大小关系

Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜Ο(2n)

注： log2n更多写成logn从左至右，时间性能依次降低。

四、复杂度如何计算

int sum=0; 执行1次

for ( int i = 0 ; i <= n ; i++){ int i = 0执行1次，i<=n执行n+2次，i++执行n+1次

sum=sum+i; 执行n+1}

1)时间分析：

该算法执行了3n+6个语句。

假设每个语句执行时间一致，均为常数t。则总时间T =（3n+6)*t。

随着问题规模n的增大，总时间的增长率与n的增长率一致，所以复杂度为O(n)。

2)结论：

• 复杂度是关于增长率的，所以可以直接忽视常数项。
• 一般可以直接关注循环段基本操作语句（示例中的sum=sum+i）的执行次数。

五、时间复杂度计算（单个循环体）

直接关注循环体的执行次数，设为k

1)算法：

int sum=0;

for ( int i = 0 ; i <= n ; i++){

sum=sum+i;}

2)解释：

i 为1 执行了1次

i 为2 执行了2次

…..

i为n 执行了n次 此时仍然满足条件

i=n+1时，跳出循环

所以循环体执行次数：k=n+1

故时间复杂度为O(n).

3)算法：

int sum=0;

for ( int i = 1 ; i <= n ; i=2*i){ sum=sum+i;} 4)解释： i 取值：1,2,4,8… 满足条件：2k≤ n K>log2n时， 跳出循环

所以循环体执行次数：[log2n]

故时间复杂度为O(logn).

六、时间复杂度计算（多个循环体）

两个运算规则：乘法规则，加法规则。

1)算法

for (i=1; i<=n; i++)

x++;

for (i=1; i<=n; i++)

for (j=1; j<=n; j++)

x++;

两个循环体是独立的，采用加法规则：

T(n)=T1(n)+T2(n)=max(T1(n),T2(n)) =O(n²)

2)算法

for ( int i = 1 ; i <= n ; i++){

for(int j=1;j<=n; j=2*j){

sum=sum+j;}}

两个循环体是嵌套的，采用乘法规则：

T(n)=T1(n)*T2(n)=O(nlogn)

七、空间复杂度计算

空间复杂度S(n)指算法运行过程中所使用的辅助空间的大小。

记为：S(n)=O(f(n))

• 辅助空间：除了存储算法本身的指令、常数、变量和输入数据外，还需要存储对数据操作的存储单元。
• 算法原地工作是指算法所需的辅助空间是常量，即O(1)。
• 考试中出现O(1)，O(n)较多。